가설검정
대립가설(연구자의 주장), 귀무가설(연구자 주장과 반대되는 모든 가설)
귀무가설에 대응하는 확률분포 설정하고 그것이 기각영역에 속하면 대립가설 채택, 아니면 귀무가설 채택
ex. 대립가설: 165이다. 귀무가설: 165보다 작거나 165보다 크다.
자유도 (df, degree of freedom)
표본을 구성하고 있는 개별 요소 중 통계적 제한을 받지 않고 자유롭게 변화될 수 있는 요소의 수
ex. 자연수 1~10에서 평균이 5되도록 표본 s5개 뽑는다,
->표본 4개는 자유롭게 정할 수 있으나, 마지막은 평균에 밪도록 조절해서 정해진다.
즉, 4개는 독립변수, 1개는 종속변수
->4의 자유도를 가진다.
교차분석
카이제곱검정
두 질적변수 간의 상관관계를 측정하는 통계적 기법으로
관찰빈도(조사결과)와 기대빈도(예상결과) 간의 차이를 측정하여 독립성, 연관성을 살펴보는 방법임.
두 빈도 차이가 적을수록 연관성 높음
귀무가설-독립이다 vs 대립가설-독립이 아니다(연관성이 있다)
(기대도수, 관찰도수, 통계량, 자유도)
ex1. 성별과 지지당의 관계
<관찰 빈도표> 남자는 공화당, 여자는 민주당을 지지한다??
| 남 | 여 | 계 | |
| 공화당 | 12 | 8 | 20 |
| 민주당 | 6 | 12 | 18 |
| 계 | 18 | 20 | 38 |
<기대빈도표>
| 남 | 여 | 계 | |
| 공화당 | 9.5 | 10.5 | 20 |
| 민주당 | 8.5 | 9.5 | 18 |
| 계 | 18 | 20 | 38 |
남자이며 공화당인 경우= 18/38*20/38*38=9.5
ex1의 설명: 위의검증량은 자유도=1을 참조해 유의수준 5%에 따른 카이제곱분포보면 3.84임,
결과: 2.66<3.84이므로 귀무가설 채택
곧, 성별과 지지당의 관계는 독립이다.
ex2. 성별과 음식 ( )는 기대빈도값, 기대빈도값이 5이하인 셀이 많음으로 적절한 결가 분석은 아님!
| 튀김 | 절임 | 구이 | 볶음 | 조림 | 계 | |
| 남 | 3(3) | 2(4) | 3(4.5) | 6(4) | 6(4.5) | 20 |
| 여 | 3(3) | 6(4) | 6(4.5) | 2(4) | 3(4.5) | 20 |
| 계 | 6 | 8 | 9 | 8 | 9 | 40 |
| 값 | 자유도 | 유의확률 | |
| Pearson Chi-Square | 6.003 | 4 | .199 |
패키지 설치
intsall,packages("gmodels")
library(gmodels)
사용법
CrossTable(row, col)
table(row, col)
chisq.test(row, col)
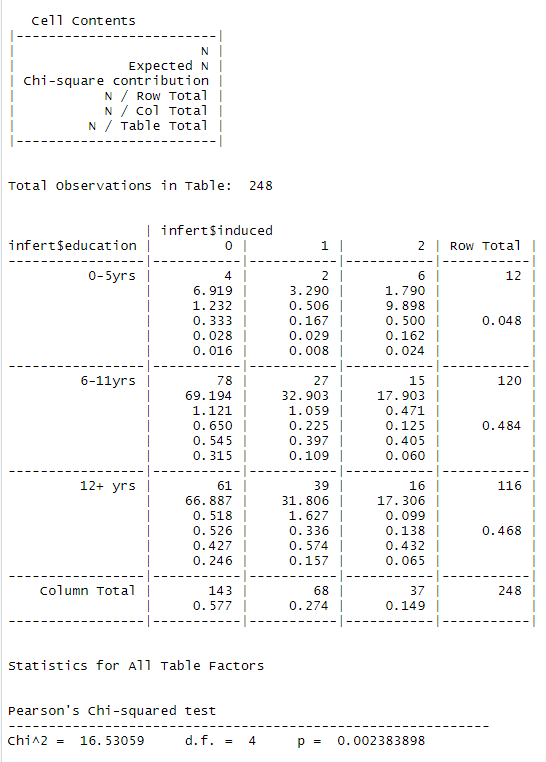
library(gmodels)
data(infert, package="datasets")
CorssTable(infert$education, infert$induced, expected=TRUE, format="SAS")
data(diamonds, package="ggplot2")
head(diamonds, 3) #첫번쨰 줄 부터 3줄까지 보여줌

CrossTable(diamonds$cut, diamonds$color, chisq=TRUE)

'R언어' 카테고리의 다른 글
| R언어: T분포-단일표본, 독립표본, 대응표본 (0) | 2019.11.23 |
|---|---|
| R언어: 분산분석 (0) | 2019.11.21 |
| R언어: 상관계수, 확률분포, 표본추출... (0) | 2019.09.28 |
| R언어 최대/소값, 최빈값, 사분위범위, 평균, 분산, 표... (0) | 2019.09.22 |
| R언어 반복, 조건, 함수 (0) | 2019.09.15 |


댓글